what it means for an object to have motion in two dimensions

In this Physics tutorial, you will learn:

• What is a projectile?
• How to divide the study of a projectile?
• What kinds of motion are involved in a projectile?
• What are the equations used during the study of a projectile?

Kinematics Learning Material

Tutorial ID	Title	Tutorial	Video Tutorial	Revision Notes	Revision Questions
iii.12	Movement in Ii Dimensions. Projectile Motion

Introduction

If you throw a stone vertically upwards, it somewhen will fall on the ground after reaching a certain height. In this instance, the object makes a one-dimensional vertical motion. Nosotros have discussed this situation in the Physics tutorial "The Meaning of Acceleration. Abiding and Non-Abiding Dispatch. Gravitational Acceleration." Nosotros take stated that this kind of motility is decelerated when the object is moving upwards and accelerated when it is moving downwards (when information technology is falling down). It is obvious the acceleration produced in this instance is caused by the gravity. Therefore, (as stated in the abovementioned tutorial), it is also known as the "gravitational acceleration" or the "acceleration of gratuitous autumn."

However, very rarely occurs that an object thrown upwards falling again at the starting signal. It is difficult to have such a precision even if you endeavour a lot. In most cases, the object will fall at another place, so its trajectory is not purely vertical. This tutorial is dedicated to such situations i.e. it deals with objects thrown at a certain angle to the horizontal direction that is different from 90° (considering if the throwing angle was 90° to the horizon, the motion would exist only vertical).

What is a projectile?

Projectile motion is a kind of motion experienced by an object that is projected about the World's surface and moves along a curved path under the activeness of gravity only (if the effects of air resistance are causeless to exist negligible). This curved path is a parabola. In the special instance when the object is thrown directly upward as discussed before, it may also be a directly line. The written report of such motions is called ballistics, and such a trajectory is known equally a ballistic trajectory. As stated before, the parabolic trajectory takes place when the object is thrown at an angle that is unlike from 90° to the horizontal management. Look at the figure below:

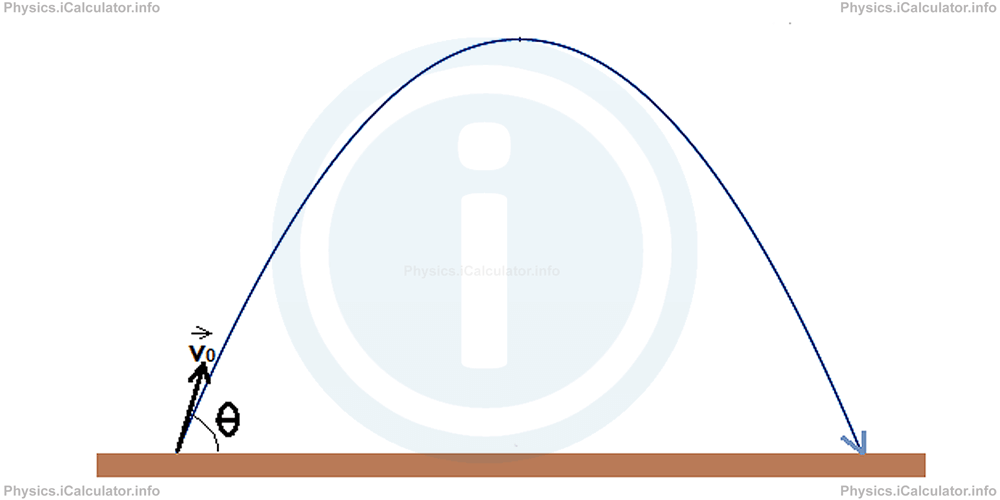
The object is thrown at initial velocity v⃗ ₀ and at an angle θ to the horizontal direction. The direction of the initial velocity vector is according the tangent to the line at the given point. Therefore, it may not testify the direction of move just touches the trajectory merely at the starting betoken. It is obvious the angle θ is dissimilar from 90°, otherwise, the object would motion only vertically. It cannot maintain the initial linear direction as shown by the vector five⃗ ₀ every bit the gravity pulls information technology down. As a effect, the object volition follow a parabolic path (information technology was kickoff demonstrated past Galileo Galilei) every bit shown in the figure above.

When the object is thrown at an angle θ to the horizontal direction, the only downwards force is the gravitational force, which tries to pull the object down. Notwithstanding, the object continues to move upward for a while due to the effect of the initial throwing forcefulness. Therefore, it will not fall immediately on the ground but it will follow a parabolic path. This parabolic path is otherwise known every bit the "trajectory" of the object.

The Physics of Projectile

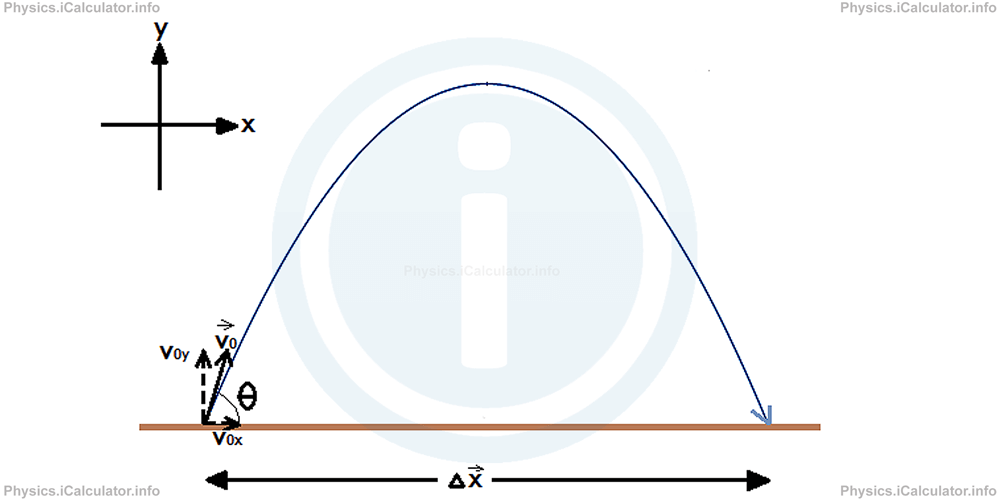
As stated in the Physics tutorial "Vectors and Scalars", when we have a state of affairs that involves at to the lowest degree ii directions, we divide the vector quantities involved in components. In this case, the initial velocity v⃗ ₀ is a vector quantity. Therefore, it is written in components where v_0x represents its horizontal component and v_0y the vertical i. This method of splitting the initial velocity into components is also used for another major reason. In absence of air resistance, the only dispatch acting on a projectile is the gravitational acceleration one thousand⃗ . We know that it is a vertical (downward) acceleration. Therefore, the horizontal function of the motion does not contain any acceleration (it is a uniform motion). Hence, information technology is necessary to study the horizontal and the vertical components of projectile separately considering the horizontal component represents a uniform motility and the vertical component a uniformly decelerated motion when moving up and a uniformly accelerated motility when falling down.

If we denote the horizontal management past x and the vertical one by y, we have for the initial velocity v⃗ ₀ :

v_0x = |5⃗ ₀| × cos θ
v_0y = |v⃗ ₀| × sin θ

If the total time of flight from the throwing position (if information technology is on the ground) until information technology falls again on the ground is t_tot, we obtain for the horizontal displacement ₀ten∆x⃗ :

∆x⃗ = five_0x × t_tot
= v₀ × cos θ × t_tot

Wait at the figure:

On the other paw, since the vertical part of motion is a motion with abiding acceleration g⃗ , we can use the four known kinematic equations to find any missing quantity required. Thus, we have

Equation one

v_y = v_0y + g × t
v_y = v₀ × sin θ + thou × t

Or

Equation 2

∆y = (v_y + v_0y) × t / 2
∆y = (v_y + v₀ × sin θ) × t / 2

Or

Equation 3

v ² _y - five ² _0y = ii × g × ∆y
five ² _y - (5₀ × sin θ )² = 2 × g × ∆y

Or

Equation 4

∆y = v_0y × t + 1000 × tⁱⁱ / two
∆y = v₀ × sin θ × t + m × t² / 2

Remarks!

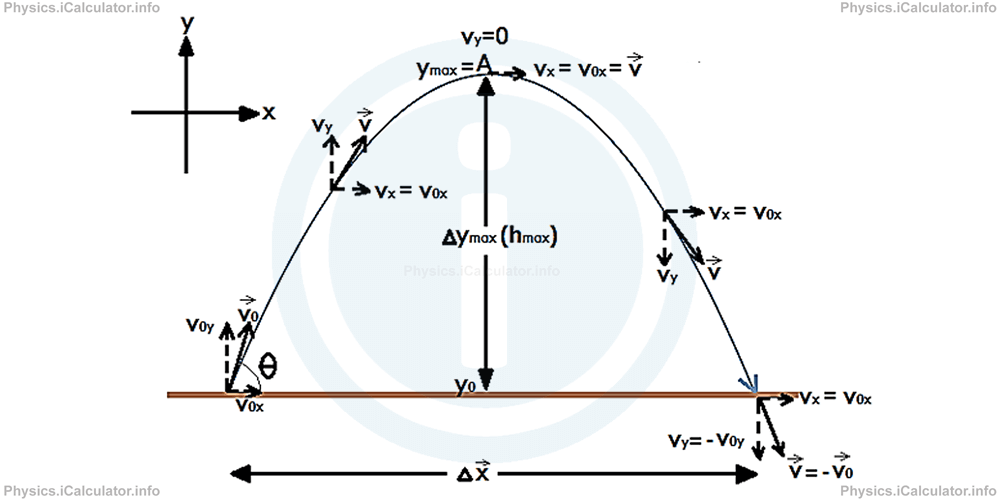
∆y here represents the change in the vertical position. It is equal to ∆y = y-y₀ where y₀ is the initial vertical position and y is the vertical position at the instant t. We often refer to ∆y every bit the height h (expect at the Physics tutorial "The Significant of Acceleration. Constant and Not-Constant Acceleration. Gravitational Acceleration."

We substitute the components v_0x and v_0y of the initial velocity by v₀ × cos θ and v₀ × sin θ respectively but nosotros cannot assign a known angle to the velocity five⃗ at any instant t because the angle changes at every instant. Therefore, we simply write v_y for the vertical component of the velocity vector v⃗ (the horizontal component v_x is known; it is v_x = v_0x = |v⃗ ₀ | × cos θ during the entire move as the horizontal component of a projectile is a uniform motion)

When the object reaches its highest position (at ∆y_max or h_max ), it stops ascension upwards and prepares to fall down. In that instant it is moving only horizontally as its vertical component of the velocity v_y is zero. Thus, if we denote the highest point of a projectile trajectory by A, we have v_yA = 0 and v_xA = |v⃗ _A | = 5₀ × cos θ.

The sign of the gravitational acceleration is taken the aforementioned as it was at the beginning of motion. Thus, if the object was thrown from the ground, the sign of g is taken equally negative during the entire motion, despite the fact that information technology accelerates in the second part of the trajectory, i.eastward. when falling down.

The equation of motion for the vertical role of a projectile is the quaternary (the last) equation listed higher up. Thus, we have

∆y = v₀ × sin θ × t + g × t² / 2
y - y₀ = v₀ × sin θ × t + m × t² / two

Or

y = y₀ + five₀ × sin θ × t + g × t² / 2

Therefore, the vertical position y every bit a office of fourth dimension t is

y(t) = y₀ + v₀ × sin θ × t + g × t² / 2

It allows us to determine the vertical position of an object at every instant t when the initial parameters (the initial vertical coordinate y₀ and the initial velocity v₀ ) are known.

The figure below includes all the abovementioned details:

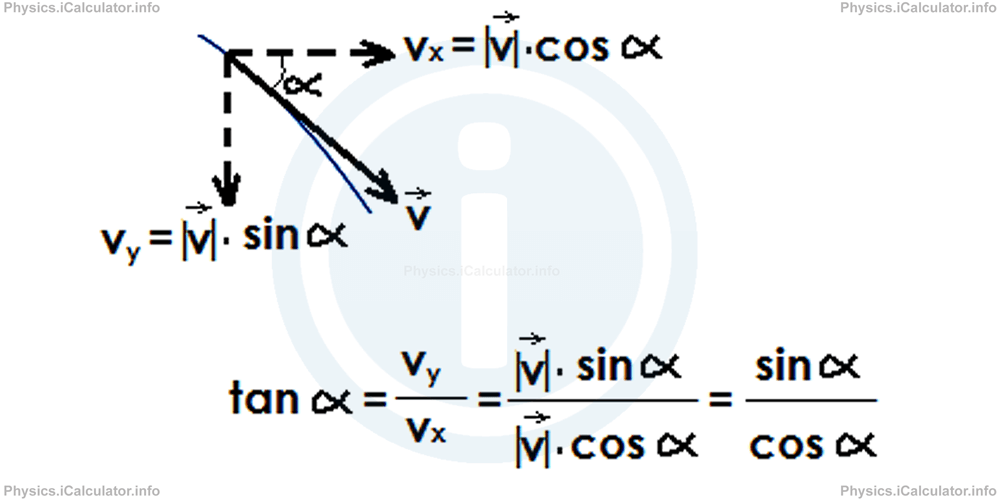
If we are interested to find the direction of the velocity vector at any given instant, we tin use the concept of the tangent of the angle formed by the velocity vector and the horizontal direction. Hence, if nosotros denote this angle by α (recollect, it is dissimilar from the initial bending θ), nosotros can write:

tan α = five_y / v_x

A small portion of the trajectory is shown in the figure below to illustrate this bespeak:

If the concluding vertical position of the object is the same as the initial one, there is a symmetry in the trajectory where the vertical line starting from the highest position can exist considered as the line of symmetry of parabola. In this case, equally discussed in the Physics tutorial "The Pregnant of Acceleration. Abiding and Not-Abiding Dispatch. Gravitational Acceleration," the relationship between the rise time t_up , the falling time t_down and the total time of flying t_total is

t_up = t_down = t_total / 2

The object is in two dissimilar instants at the same vertical position (height) during a projectile motion: one when it is rising up and the other when it is falling down. Unlike in the pure vertical movement, the object is in unlike horizontal positions in these 2 instants, so we have two distinct points Thou and Northward in the space in which the object is at the same height. Their coordinates are M(_xM, _yM) and North(_xN, _yN) respectively, where _yM = _yN . Look at the figure:

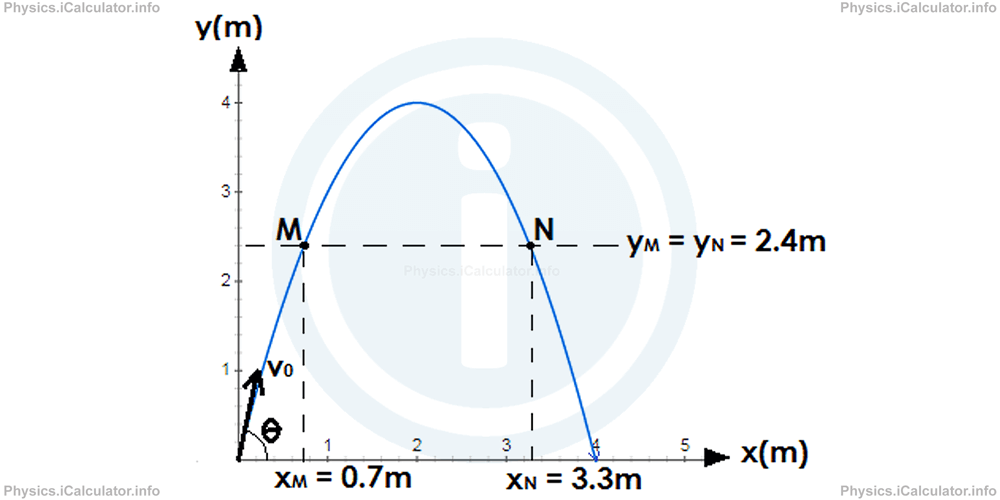
(The values obtained for the horizontal coordinates are rounded to 1 decimal place)

Let's consider at an example using the clues of the trajectory shown in the above figure.

Example 1

An object is moving co-ordinate to a ballistic trajectory equally shown in the effigy.

Calculate:

1. The total time of flight
2. The magnitude of the initial velocity
3. The bending θ formed by the initial velocity vector and the horizontal management
4. The coordinates of the object at t = 0.three s
5. The instant(s) in which the object is at y = 3m

Solution 1

We can obtain some useful information from the figure. Thus, nosotros encounter that the initial position of the object is at (0, 0). This ways x₀ = 0 and y₀ = 0.

Also, it is obvious the object reaches its maximum position at yA = y_max = 4m. The corresponding horizontal coordinate is xA = 2m.

Yet, the maximum horizontal displacement is Δx_max = 4m as the object falls on the footing at that horizontal position.

Before starting with the solution, let's complete the figure with the information obtained in a higher place. (For simplicity we have the magnitude of gravitational dispatch equal to 10 m/southward².)

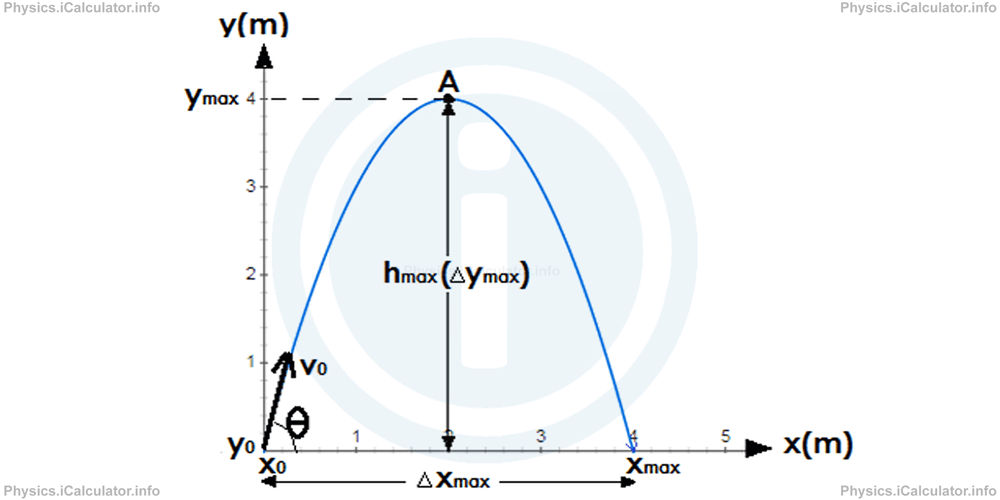
Nosotros apply the info obtained for the indicate A to calculate the total time of flight t_tot. We have:

v ² _yA - v ² _0y = two × g × ∆y_max

Substituting the values, we obtain

0² - v ^two _0y = 2 × (-ten) × 4
-v ^two _0y = -80
five_0y = √80grand/southward ≈ 8.94 thou/south

Now, we can summate the rising fourth dimension tup. We take:

∆y_max = (v_yA + v_oy)t_upwards / 2

Substituting the values (and giving that v_yA = 0), nosotros obtain

4 = (0 + √80 × t_up / two
8 = √fourscore × t_up
t_upward = eight / √80 = √viii × √8 / √8 × √x = √ 8 / 10 = 0.89 southward

Therefore, by symmetry it is obvious the total time of flying is

t_tot = 2 × t_up = two × 0.89 s = ane.78 southward

We demand to know the horizontal component of the initial velocity five_0x in order to calculate its magnitude subsequently. We accept

∆x_max = v_0x × t_tot

Substituting the known values, we obtain

4m = v_0x × ane.78 s
5_0x = iv one thousand / one.78 s = 2.25 m/due south

Therefore, applying the known equation

|5⃗ ₀ | = √five_0x ² + five ² _0y

we obtain for the magnitude of the initial velocity:

|v⃗ ₀ | = √√fourscore ^two + 2.25^two
= √lxxx + 6.25
= √86.25
= 9.29 k/s

The initial angle θ is calculated using the concept of tangent of the angle θ formed by the initial velocity vector and the horizontal management. Nosotros accept

tan θ = five_0y / v_0x = viii.94 / 2.25 = iii.97

Hence,

θ = arctan 3.97 = 75.9⁰

At t = 0.3, we have

ten(t) = 5_0x × t

and

y(t) = y₀ + 5_oy × t + g × t² / ii

Substituting the known values, nosotros obtain

x(0.3) = 2.25 × 0.three
= 0.675m

and

y(0.3) = 0 + 8.94 × 0.3 + (-x) × 0.3ⁱⁱ / 2
= ii.682m - 0.450m
= 2.232m

Hence, at t = 0.3s the object is at (0.675m, 2.232m). This means information technology is 0.675 yard on the correct and ii.232 grand higher up the starting point.

As stated before, the object is in two instants at the aforementioned tiptop during a projectile. Therefore, we must use the quadratic equation of motion

y(t) = y₀ + v_oy × t + chiliad × t² / 2

to calculate the required instants t. Thus, substituting the values, we obtain

3 = 0 + 8.94 × t + (-10) × t² / 2
-5 × t² + 8.94 × t - iii = 0

Dividing both sides by (-five), nosotros obtain

t² - 1.788 × t + 0.6 = 0

Using whatsoever of the methods for solving quadratic equations, nosotros obtain

t₁ = 0.45s and t₂ = 1.34s

Now, let'south see what happens if an object thrown at an bending θ to the horizontal direction does not end its motion at the aforementioned level (pinnacle) but higher up or beneath the starting point. To illustrate this bespeak we take used the numerical example beneath:

Case 2

A ball is kicked at 15 m/s from the terrace of a 12 k high building. The bending of the initial velocity with the horizon is 370. Ignore the air resistance and accept the magnitude of k⃗ equal to x g/southward². As well, have cos 370 = 0.eight and sin 370 = 0.vi.

Summate:

1. The maximum height (from the ground) the object tin reach.
2. What is the total time of flight?
3. How many metres away from the building is the ball when information technology touches the basis?
4. What is the brawl'southward velocity just earlier touching the ground?

Solution 2

The figure below helps creating a clearer idea about the motility described in the problem.

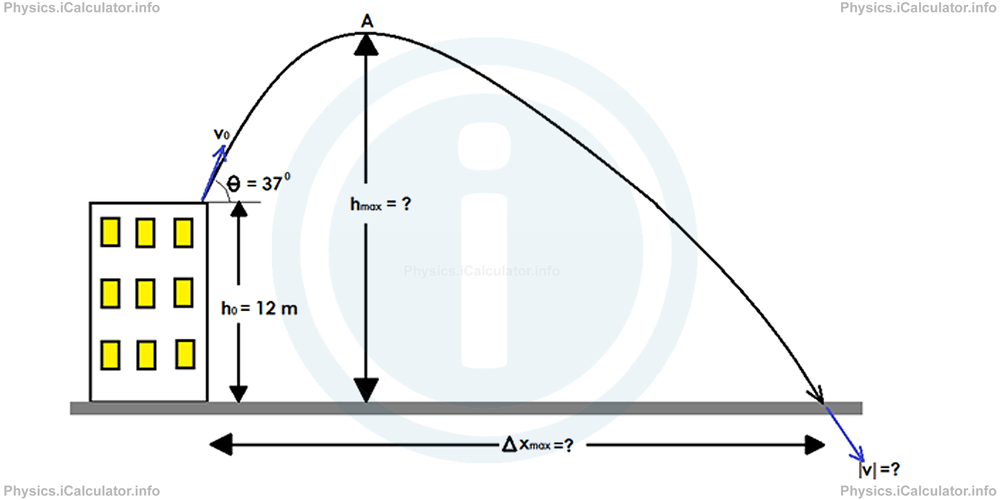
To summate the maximum height hmax, showtime we have to calculate the actress height h1 above the edifice and then add it with the edifice'southward summit h0. We have:

v ² _yA - five ² _0y = 2 × g × h_i

We know that

5_0x = 5₀ × cos θ = fifteen × 0.eight = 12 m/s
five_0y = 5₀ × sin θ = 15 × 0.half dozen = ix m/s
v_yA = 0

and

g = -10 m/southward²

Therefore, we obtain after the substitutions:

0² - 9² = 2 × (-10) × h_i
-81 = -20 × h₁
h₁ = -81 / -twenty = four.05 thousand

Hence, the maximum height the object can reach is

h_max = h₀ + h_one
= 12m + iv.05m
= sixteen.05m

We can utilise the equation of projectile

y(t) = y₀ + v_oy × t + grand × t² / 2

for computing the total time of flight t. Thus, giving that at the end of move the position of the object will be y = 0, we obtain afterward substituting the known values,

0 = 12 + ix × t + (-10) × t² / 2
-5 × t² + 9 × t + 12 = 0
v × t²-9 × t - 12 = 0

We have a quadratic equation (with variable t) which has its constants: A = 5, B = -9, C = -12. Therefore, we have

∆ = B² - 4 × A × C
= (-9)^two - 4 × 5 × (-12)
= 81 + 240
= 321

Therefore, we take

t_i = -B - √∆ / 2 × A
= - (-9) - √321 / 2 × 5
= 9 - 17.9 / 10
= -viii.9 / 10
= -0.89 southward

This effect is negative. But the time cannot be negative, then this value is automatically rejected. The second solution is

t_two = -B + √∆ / ii × A
= -(-9) + √321 / 2 × 5
= nine + 17.ix / x
= 26.nine / 10
= 2.69 southward

Hence,

t_tot = t2 = 2.69 s

"How many metres away from the building is the ball when it touches the footing?" means: "calculate the total horizontal displacement ∆10⃗ of the object."

Therefore, we have:

∆ten⃗ = five⃗ _0x × t_tot
= 12 m / s × 2.69 s
= 32.28 m

To calculate the magnitude of the object'southward concluding velocity simply before touching the ground, nosotros demand its components five₁₀ and v_y . One of them (v₁₀ ) is already known equally v₁₀ = five_0x = 12 m/southward. As for the vertical component of the final velocity v_y , we have

v ² _y - five ² _0y = 2 × g × ∆y

In our example ∆y = -12m as at the terminate of motion, the object is 12 yard below the original meridian. Also, nosotros take chiliad = - ten m/s² as initially it was so. Therefore, we obtain after substitutions:

v ² _y -ix² = 2 × (-10) × (-12)
v ² _y - 81 = 240
5 ⁱⁱ _y = 240 + 81 = 321
v_y = √321
= 17.9 grand/south

Now, using the equation

|v⃗| = √v_x ^two + v ² _y

we can summate the magnitude of the final velocity when the object is but touching the ground. Thus,

|v⃗| = √12^two + 17.9ⁱⁱ
= √144 + 321
= √465
≈ 21.half-dozen thou/south

Whats side by side?

Enjoy the "Move in 2 Dimensions. Projectile Motion" physics tutorial? People who liked the "Motion in Ii Dimensions. Projectile Motion" tutorial found the following resources useful:

1. Physics tutorial Feedback. Helps other - Leave a rating for this tutorial (see below)
2. Kinematics Revision Notes: Movement in 2 Dimensions. Projectile Move. Print the notes so you tin can revise the key points covered in the physics tutorial for Motion in Ii Dimensions. Projectile Motion
3. Kinematics Practice Questions: Motion in 2 Dimensions. Projectile Move. Test and ameliorate your knowledge of Motion in Two Dimensions. Projectile Motion with example questins and answers
4. Bank check your calculations for Kinematics questions with our fantabulous Kinematics calculators which contain full equations and calculations clearly displayed line past line. Meet the Kinematics Calculators past iCalculator™ below.
5. Continuing learning kinematics - read our next physics tutorial: Relative Motility

Kinematics Calculators

The following Physics Calculators are provided in support of the Kinematics tutorials.

• Uniform Motion Figurer
• Uniformerly Accelerated Decelerated Movement Calculator
• Projectile Motion Estimator

Physics Calculators

You lot may besides detect the post-obit Physics calculators useful.

• Cocky Inductance Figurer
• Coefficient Of Finesse Figurer
• Kepler Third Police Estimator
• British indian ocean territory Savart Police force Calculator
• Magnetic Field Inside A Solenoid Calculator
• Drag Force On Disk Calculator
• Capacitor Energy Calculator
• Logic Gates Operations Calculator
• Gravitational Potential Energy Physics Calculator
• Electric Field Of Line Charge Calculator
• Antenna Aperture Reckoner
• Pipe Diameter Estimator
• Charge Density Calculator
• Current In A Rl Circuit Reckoner
• Capacitors Power Factor Correction Estimator
• Focal Length Of Optical Convex Figurer
• Voltage Divider Calculator
• Capacitance Of Cube Computer
• Capacitance Of Circular Solid Cylinder Calculator
• Black Hole Gravitational Redshift Calculator

harrisdidan1966.blogspot.com

Source: https://physics.icalculator.info/kinematics/projectile-motion-in-two-dimensions.html

Share this post